Regular Lattice Polygons Don't Exist
That is, besides squares. I’ll prove it.
Regular n-gons, for \(n \geq 5\) and \(n \neq 6\)
We can pretty easily construct an infinite descent proof for regular polygons with obtuse angles. We’ll start with this:
Lemma: If three vertices of a parallelogram are lattice points, then the fourth is also.
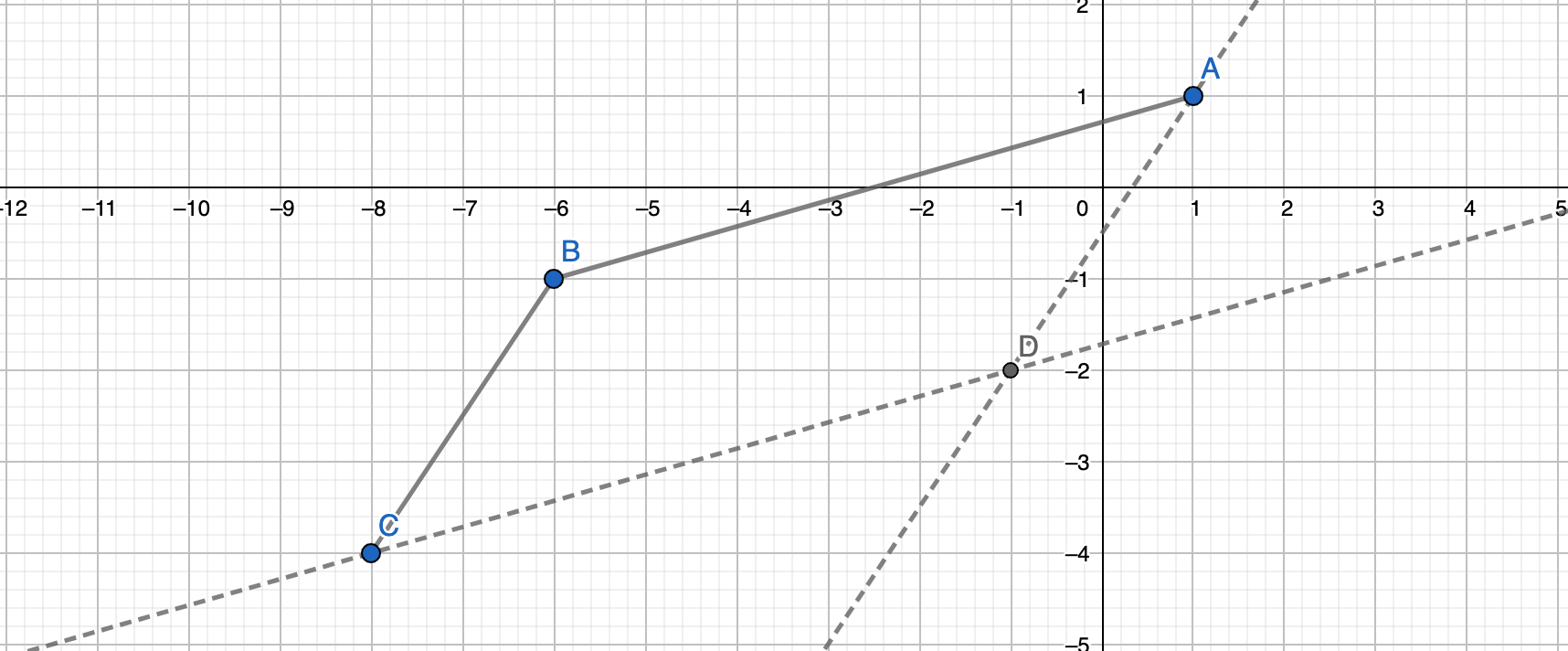
This follows from an argument of vector addition. Let’s say \(A, B, C\) are all known lattice points in parallelogram \(ABCD\). Treating points as vectors with integer components, we have \(A-B = D-C\).
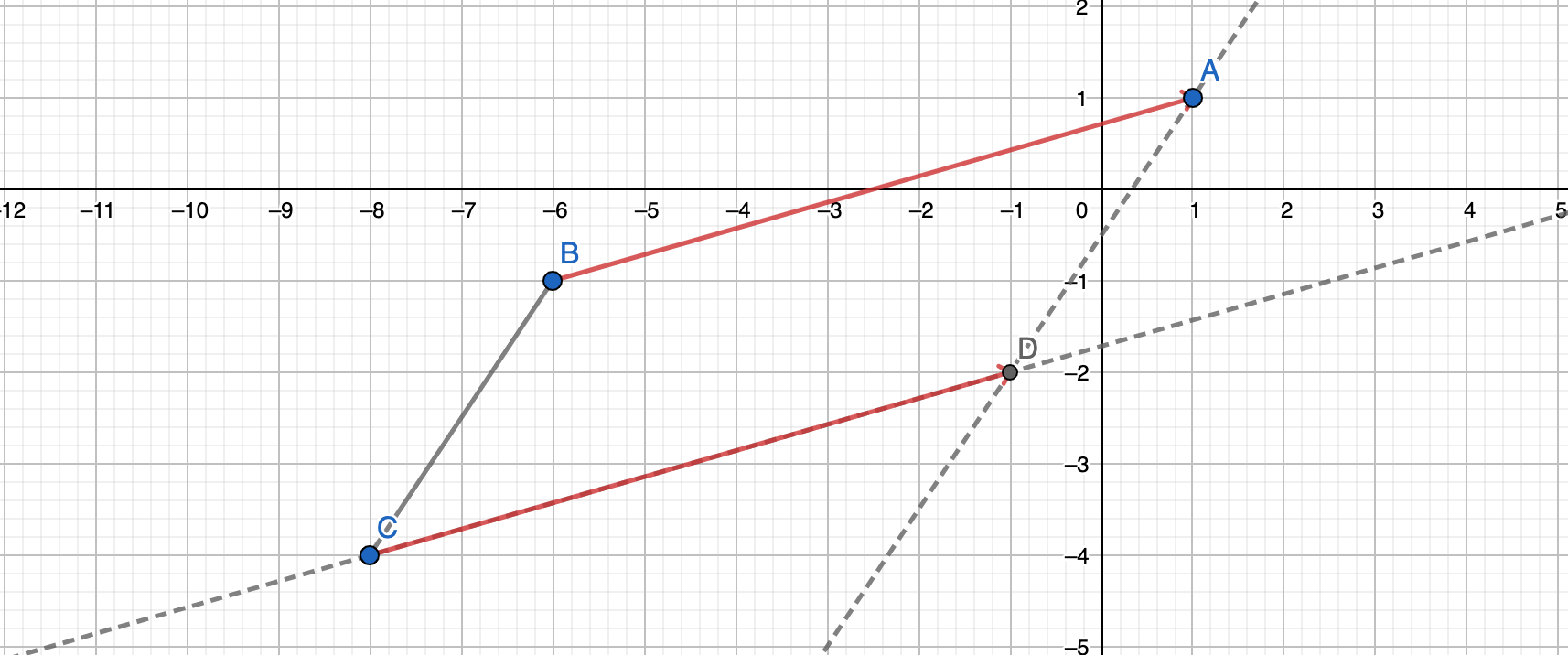
\(A-B\) is a vector with integer components, therefore so is \(D-C\), and since \(C\) has integer components, so does \(D\).
Now, let’s consider reflecting each vertex of a regular \(n\)-gon over a subtending diagonal:
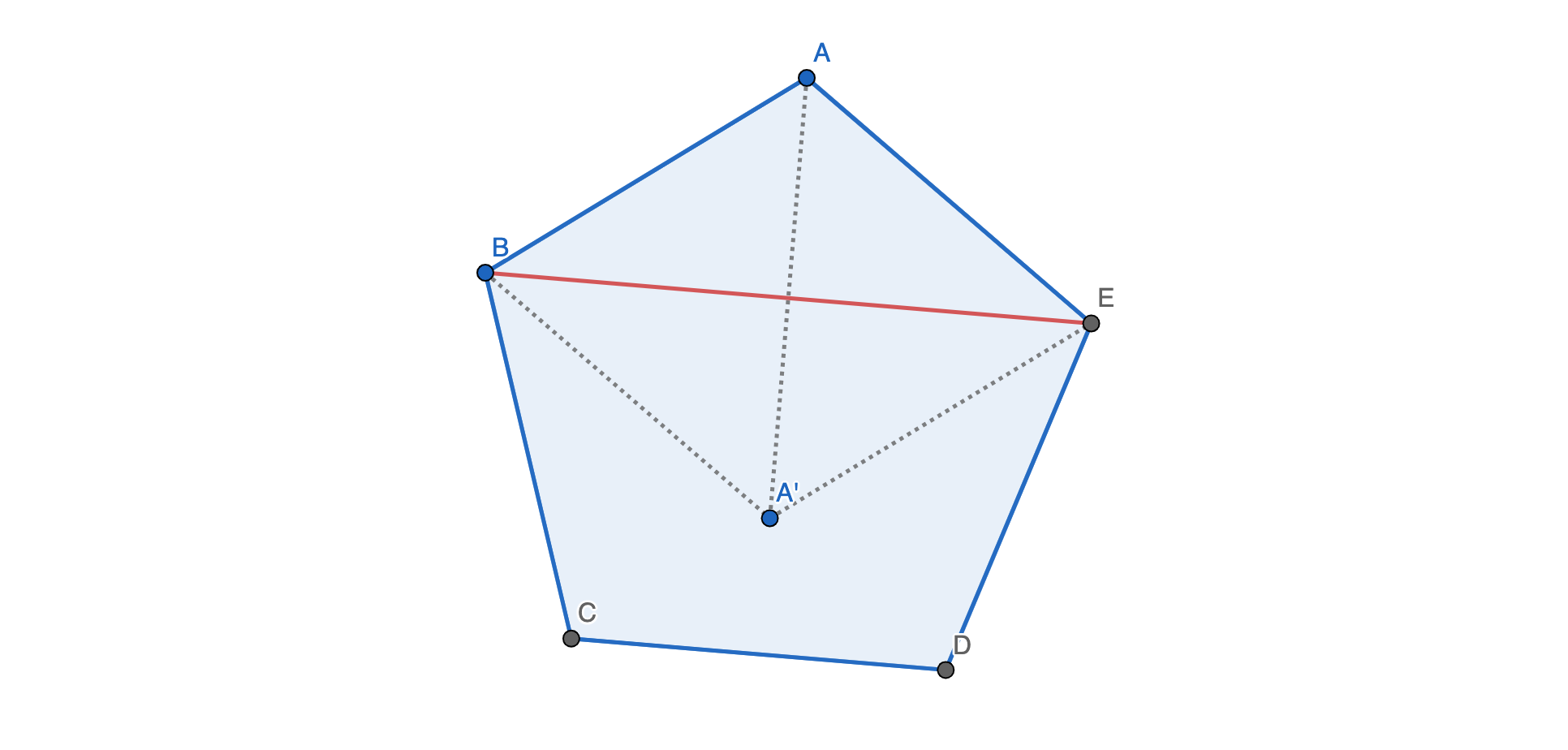
When we do so, we know the reflected point will be within the polygon, as the interior angles are obtuse and \(\angle AEA'\) and \(\angle ABA'\) are strictly acute.
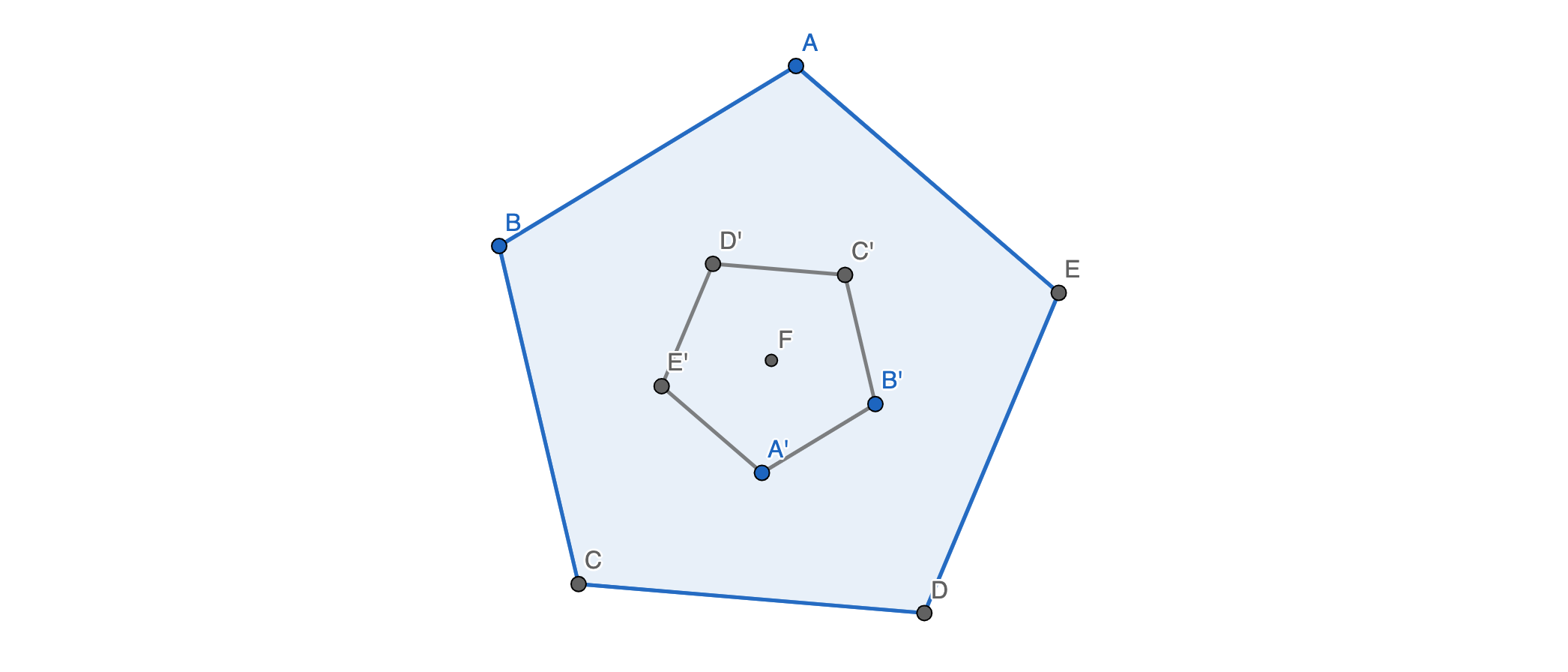
When we do this for each vertex, we constructed five points that are rotationally symmetric about the polygon’s center, and strictly within the polygon. So, we’ve constructed a smaller regular \(n\)-gon. Moreover, each reflection formed a lattice parallelogram, so this smaller \(n\)-gon is also lattice. This will fail as we repeat this process on our recently constructed regular \(n\)-gon each time, as the side length will eventually have to be less than \(1\), so we reach a contradiction.
Problem?
I like this proof, but the only problem is that it doesn’t work for \(n = 3\) or \(n = 6\).
Why not \(n=6\)? Because the above proof assumed that the smaller \(n\)-gon is not degenerate. Note that there’s exactly one edge case in which all reflected points land at the center of the polygon; this is only true when the interior angle measure of the polygon, \(x\) satisfies \(180-x = x/2\).
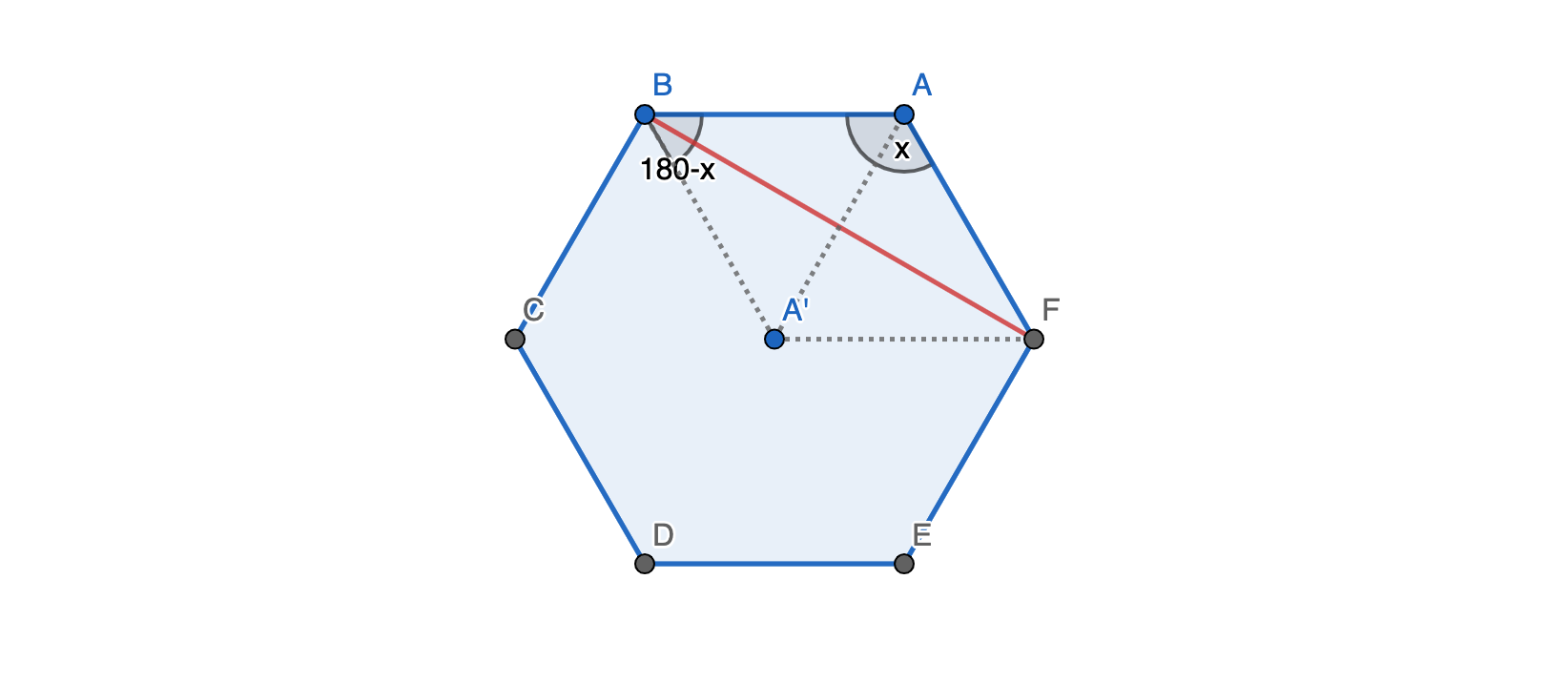
That would imply that \(A'B, A'F\) are angle bisectors of \(\angle CBA, \angle AFE\), respectively, so they meet at the polygon’s center.
And why not \(n=3\)? Because if we attempt the same process, we end up with a larger equilateral triangle.
Alternate Solution
We can tackle these cases with a different approach. First, let’s establish that the cases of \(n = 3\) and \(n = 6\) are actually the same. If it were possible for \(n=6\), then we can pick every other vertex to form an equilateral triangle. If it were possible for \(n=3\), then we could continuously reflect one vertex about the opposite side and essentially construct a tiling of lattice equilateral triangles (lattice by our lemma) in which a regular hexagon will exist.
So, let’s just disprove it for \(n=3\) using Pick’s Theorem.
Pick’s Theorem states that for any lattice polygon, the area is equivalent to \(I + \frac{B}{2} - 1\), where \(I\) is the number of lattice points strictly inside the polygon, and \(B\) is the number of lattice points on the boundary (There are a lot of long and complicated proofs of this theorem; this talk contains a pretty cool one by Tadashi Tokieda). By this theorem, we’ll only need to know that this means any lattice polygon has area that is either an integer or half-integer.
Now, the formula for the area of an equilateral triangle with side length \(s\) is \(\frac{s^2\sqrt{3}}{4}\). Given that the triangle has integer coordinates, by Pythagorean Theorem its side length must the the square root of an integer, let’s say \(\sqrt{k}\). Then the area is \(\frac{k\sqrt{3}}{4}\), which is always irrational. This contradicts with the assumption of Pick’s Theorem.
Other Notes
Here are a few things I might look into in the future:
- In a hexagonal lattice, there are no regular lattice polygons other than triangles and hexagons.
- Regular lattice triangles and hexagons exist in \(3\)-space.
- Follow up: what other regular lattice polygons exist in \(3\)-space, or in \(>3\) -space?